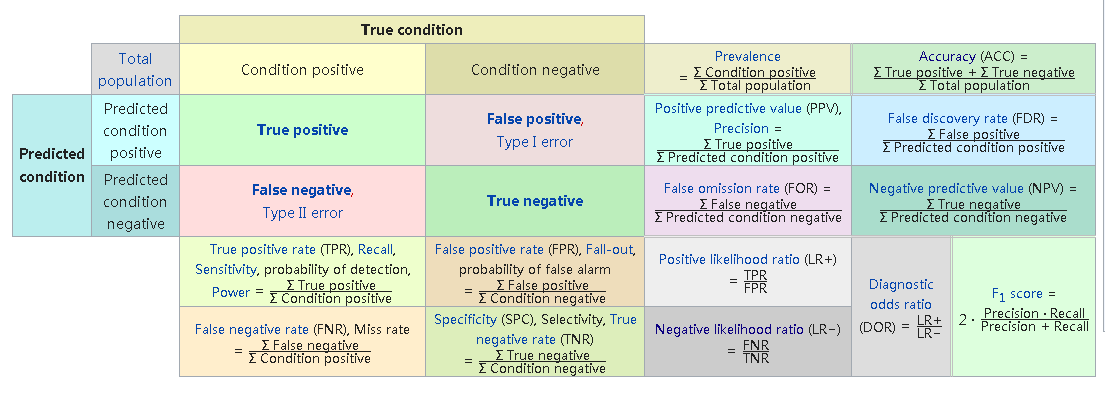
Classification

混淆矩阵

True/False: 预测的结果是否正确。
positive/negative: 预测结果，预测为正例还是反例。
由混淆矩阵延伸出来的评价指标有：Accuracy, Precision, Recall, F1, TPR, FPR, ROC/AUC等。
对于多分类问题，通常计算每一个类别的混淆矩阵（P：属于A类，N：不属于A类），然后可以把每一类的指标聚合起来，求出一个总的指标。

# Examples
from sklearn.metrics import confusion_matrix
import numpy as np

y = np.random.randint(0, 2, 20)
pred = np.random.randint(0, 2, 20)
print(confusion_matrix(y, pred))

Accuracy

精度，样本预测正确的数量除以总样本数。

计算方法：$y_i$是第$i$个样本的标签，$\hat{y_i}$是第$i$个样本的预测标签，$n$是样本数量
$$
\begin{equation}
\begin{aligned}
\text{accuracy}(y,\hat{y}) = \frac{1}{n}\sum\limits_{i=1}^{n}1(\hat{y}_i=y_i)
\end{aligned}
\end{equation}
$$

使用混淆矩阵计算:
$$
\begin{equation}
\begin{aligned}
\text{accuracy}=\frac{\text{TP}+\text{TN}}{\text{TP}+\text{TN}+\text{FP}+\text{FN}}
\end{aligned}
\end{equation}
$$

多标签计算:

如果一个样本对应多个标签，那么可以设置样本的所有标签都对的上才表示分类正确的规则来计算accuracy。

缺点:

在样本不平衡的条件下，准确率不能很好的衡量模型的效果，比如正样本占90%，负样本10%，如果模型把全部样本都判断为正样本，那么模型的准确率也有90%，可能也会觉得很好。

# Examples
from sklearn.metrics import accuracy_score
import numpy as np

# single label
y = np.random.randint(0, 2, 20)
pred = np.random.randint(0, 2, 20)
print(accuracy_score(y, pred))

# multilabel
print(accuracy_score(np.array([[1,1], [0, 0]]), np.ones((2, 2))))

Balanced Accuracy

计算:在二分类情况下，
$$
\begin{equation}
\begin{aligned}
\text{balanced_accuracy}=\frac{\text{TPR+TNR}}{2}
\end{aligned}
\end{equation}
$$

其中$\text{TPR}=\frac{\text{TP}}{\text{TP+FN}}=\text{Recall}$，可以理解为模型对正样本的识别率（覆盖率）；$\text{TNR}=\frac{\text{TN}}{\text{TN+FP}}$，可以理解为模型对负样本的识别率（覆盖率）。Balanced accuracy取TPR和TNR的平均，可以避免不平衡数据集对模型评估的影响。

特点:

在平衡数据集上，balanced accuracy的等价于accuracy。
如果模型在每个类别的性能一样（即TPR=TNR），balanced accuracy也等价于accuracy。

from sklearn.metrics import balanced_accuracy_score
y = [0, 1, 0, 0, 1, 0]
pred = [0, 1, 0, 0, 0, 1]
balanced_accuracy_score(y, pred, adjusted=False) # 0.625

Precision

计算:
$$
\begin{equation}
\begin{aligned}
\text{Precision} = \frac{\text{TP}}{\text{TP}+\text{FP}}
\end{aligned}
\end{equation}
$$

特点：

在二分类中，如果划分阈值越大，那么被划分为正样本的“门槛”越高，Precision（查准率）越大。

# Examples
from sklearn.metrics import precision_score
y = np.random.randint(0, 2, 20)
pred = np.random.randint(0, 2, 20)
precision_score(y, pred)

Recall

计算:
$$
\begin{equation}
\begin{aligned}
\text{Recall} = \frac{\text{TP}}{\text{TP}+\text{FN}}
\end{aligned}
\end{equation}
$$

特点:

在二分类中，划分阈值越小，更多的样本被划分为正样本，那么正样本的覆盖率就越大，Recall（查全率）越大。

# Examples
from sklearn.metrics import recall_score
y = np.random.randint(0, 2, 20)
pred = np.random.randint(0, 2, 20)
recall_score(y, pred)

F1 score

计算:
$$
\begin{equation}
\begin{aligned}
\text{F1}=\frac{2\text{Precision}*\text{Recall}}{\text{Precision}+\text{Recall}}
\end{aligned}
\end{equation}
$$

特点:

取F1 score最高的划分阈值，可以平衡Precision和Recall。

# Examples
from sklearn.metrics import f1_score
y = np.random.randint(0, 2, 20)
pred = np.random.randint(0, 2, 20)
f1_score(y, pred)

ROC

在样本集中，经过模型预测后得到每个样本判断为正例的概率值，然后遍历所有概率值为划分阈值，每个阈值会把样本划分为正例和反例，加上样本的标签可以计算出混淆矩阵，然后根据公式计算TPR和FPR。TPR和FPR的计算如下

TPR: 真正率，$\frac{\text{TP}}{\text{TP+FN}}$，TPR只关心正样本中有多少被正确覆盖了。

FPR: 假正率，$\frac{\text{FP}}{\text{FP+TN}}$，FPR只关心负样本有多少被错误覆盖了。

ROC(Receiver Operating Characteristic)的横坐标是FPR，纵坐标是TPR，如下图：

图2 ROC曲线

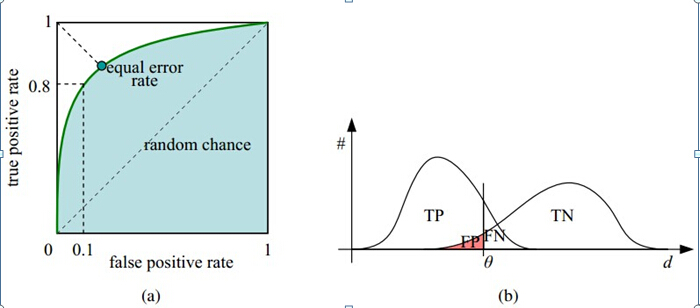
ROC曲线的阈值问题：ROC曲线是遍历所有阈值来绘制整条曲线的，如果我们不断遍历所有阈值，预测的正样本和负样本是在不断变化的，相应地会产生不断变化的(FPR,TPR)点对，这些不同的(FPR,TPR)点对构成了ROC曲线。

图3 ROC曲线--遍历阈值

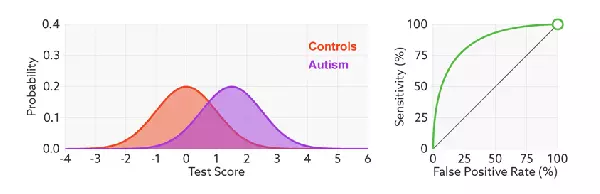
如何判断ROC曲线的好坏: FPR表示模型虚报正例的相应程度，TPR表示模型预测正例的覆盖程度，所以希望：虚报的正例越少越好，覆盖的正例越多越好。综合就是TPR越高，同时FPR越低，即ROC曲线越陡，模型的性能越好。

图4 ROC曲线--效果好坏

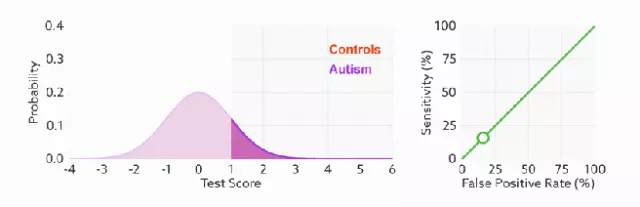
ROC曲线无视样本不平衡: 因为ROC中的TPR和FPR分别关心正样本覆盖程度和负样本误判程度，两个指标跟正负样本的比例没有关系。

图5 ROC曲线--样本比例关系

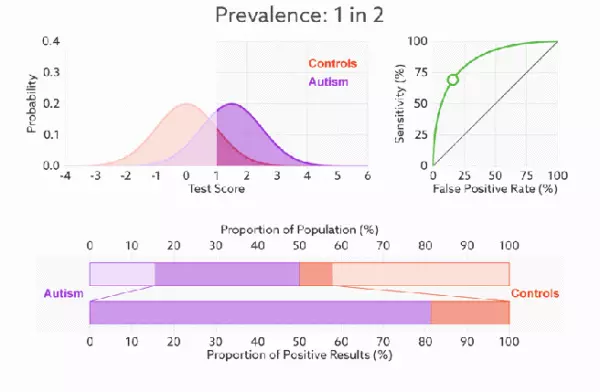
特点:

ROC曲线可以比较两个模型的效果，将两个模型的ROC曲线画在同一个图上，上面的曲线比下面的曲线要好，然而这样只能定性的看（从图像上看），如果要定量的看，可以使用AUC（Area Under Curve），即ROC曲线下的面积。

AUC(Area Under Curve)

AUC是ROC曲线下的面积

AUC的含义：随机给定一个正样本和负样本，分类器输出该正样本为正的概率值比分类器输出该负样本为正的概率值要大的可能性

特点: AUC可以避免设定一个阈值，将概率值转换成类别，直接从模型预测样本的概率上去评判模型的优劣。但是AUC只能用于二分类任务。在很多模型上，AUC可以作为跟logloss一样的优化目标，来训练模型

AUC的计算:

按概率值从高到矮排个降序（概率值越高，排序值越大），对于正样本中概率最高的那个，排序为rank_1，比它概率小的有M-1个正样本（M为正样本个数），(rank_1 - M + 0)个负样本
正样本概率第二高的，排序为rank_2，比它概率小的有M-2个正样本，（rank_2-M+1）个负样本
正样本概率第三高的，排序为rank_3，比它概率小的有M-3个正样本，（rank_3-M+2) 个负样本
一次类推，正样本中概率最小的，排序为rank_M，比它概率小的有M-M=0个正样本，（rank_M-M+M-1)=(rank_M-1)个负样本
总共有M*N个正负样本对（M为正样本数量，N为负样本数量）。把所有比较中正样本概率大于负样本概率的例子都算上，得到公式（rank_1-M + rank_2-M+1 + rank_3-M+2 + … + rank_M-M+M-1)/(M*N)，就是正样本概率大于负样本概率的可能性了。如下式

$$
\begin{equation}
\begin{aligned}
\text{AUC} & = \frac{(rank_1-M)+(rank_2-M+1) + (rank_3-M+2) + … + (rank_M-M+M-1)}{M\times N} \\
& = \frac{(rank_1+rank_2+rank_3+…+rank_M)-(M+M-1+M-2+…+1)}{M\times N} \\
& = \frac{\sum_{ins_i\in \text{positiveclass}}rank_{ins_i} - \frac{M\times (M+1)}{2}}{M\times N}
\end{aligned}
\end{equation}
$$

简单讲，就是所有正样本在所有样本的排序的序号加起来，减去正样本在正样本的序号和，再除以正样本数量乘以负样本数量

# 手动计算ROC和AUC
import matplotlib.pyplot as plt
from sklearn.metrics import *

y = np.random.randint(0,2, 100)
pred = np.random.uniform(size=100)

# 计算ROC
TP_list = list()
TN_list = list()
FP_list = list()
FN_list = list()
tpr = list()
fpr = list()

for threshold in np.linspace(start=0, stop=1, num=500): # 此处应该是遍历pred的排序后的值
    y_pred = [1 if item >= threshold else 0 for item in pred]
    confuse_matrix = confusion_matrix(y, y_pred)
    TP_list.append(confuse_matrix[1,1])
    TN_list.append(confuse_matrix[0,0])
    FN_list.append(confuse_matrix[1,0])
    FP_list.append(confuse_matrix[0,1])
    
    tpr.append(TP_list[-1]/(TP_list[-1]+FN_list[-1]))
    fpr.append(FP_list[-1]/(FP_list[-1]+TN_list[-1]))

# 计算AUC
pred_true = [[pred[i],y[i]] for i in range(len(pred))] # 合并预测概率值和真实标签
pred_true = sorted(pred_true, key=lambda x:x[0]) # 对预测概率值进行升序
rank_index = list(range(1, len(pred)+1)) # 所有样本的序号

M = sum(np.array(y)==1) # 正样本个数
N = sum(np.array(y)==0) # 负样本个数

# 计算正样本index和
sum_pos_index = sum([rank_index[i] if pred_true[i][1]==1 else 0 for i in range(len(pred_true))])
# 根据公式计算AUC
AUC = (sum_pos_index - M*(M+1)/2)/(M*N)


import matplotlib.pyplot as plt
plt.figure()
lw = 2
plt.plot(fpr,tpr,  color='darkorange',
         lw=lw, label='ROC curve (area = %0.2f)' % AUC)
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('手动计算ROC和AUC')
plt.legend(loc="lower right")
plt.show()


# 使用sklearn计算ROC和AUC
fpr, tpr,_ = roc_curve(y, pred)
auc_score = auc(fpr, tpr)

plt.figure()
lw = 2
plt.plot(fpr,tpr,  color='darkorange',
         lw=lw, label='ROC curve (area = %0.2f)' % auc_score)
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('调包计算ROC和AUC')
plt.legend(loc="lower right")
plt.show()

图6 计算ROC-AUC

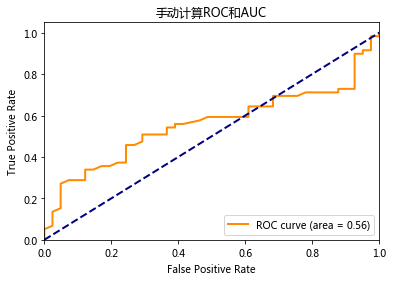
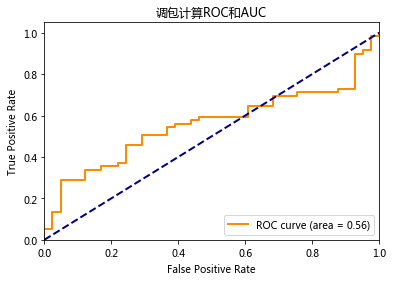
Average Precision(AP)

计算:
$$
\begin{equation}
\begin{aligned}
\text{AP}=\sum_n(R_n - R_{n-1})P_n
\end{aligned}
\end{equation}
$$
其中，$P_n$和$R_n$是第n个threshold的precision和recall

from sklearn.metrics import average_precision_score
y = np.random.randint(0,2, 100)
pred = np.random.uniform(size=100)
average_precision_score(y, pred)

mean Average Precision(mAP)

在CV问题中，mAP先计算每个类别的AP，然后再求个平均

计算:
$$
\begin{equation}
\begin{aligned}
\text{mAP} = \frac{\sum\limits_{q=1}^Q \text{average_precision}(q)}{Q}
\end{aligned}
\end{equation}
$$

brier score loss

计算: 对于二分类，正负标签分别为0-1，brier score分别计算正样本的预测输出概率值与1、负样本的预测输出概率值与0的差的平方和，再除以样本总数

特点

score越小越好

from sklearn.metrics import brier_score_loss
import numpy as np

y_true = np.array([0, 1, 1, 0])
y_true_categorical = np.array(["spam", "ham", "ham", "spam"])
y_prob = np.array([0.1, 0.9, 0.8, 0.3])
brier_score_loss(y_true, y_prob) # (0.1**2 + 0.1**2 + 0.2**2 + 0.3**2)/4

neg log loss

负对数似然损失

如果是二分类，y是0-1标签：样本X只有一个概率值p，表示样本属于正样本的概率；标签y=1表示正样本，y=0表示负样本，那么单个样本loss计算如下
$$
\begin{equation}
\begin{aligned}
\text{neg_log_loss} = -(y\log(p)+(1-y)\log(1-p)
\end{aligned}
\end{equation}
$$
如果是二分类或多分类，数据集有几个类别，样本X就有几个概率值，分别表示样本X属于不同类别的概率；标签Y，可以是类别的index，也可以是onehot后的编码，那么属于第C类的样本X的loss计算如下
$$
\begin{equation}
\begin{aligned}
\text{neg_log_loss} = -\log(p[C])
\end{aligned}
\end{equation}
$$

第一个公式只用了一个概率值p来表示样本X属于正样本的概率，如果X是正样本，loss为$-\log(p)$，如果X是负样本，loss为$-\log(1-p)$；第二个公式用了多个概率值，分别表示样本X属于不同类别的概率，所以不管样本属于哪一类，只需要计算那一类的概率值的对数的负数，即$-\log(p[C])$

对于多个样本，一般把单个样本的loss进行求平均

from sklearn.metrics import log_loss
log_loss(["spam", "ham", "ham", "spam"],
         [[.1, .9], [.9, .1], [.8, .2], [.35, .65]]) 
# -(np.log(0.9)*2+np.log(0.8)+np.log(0.65))/4

jaccard score

计算: 假设第i个样本的真实标签为$y_i$，预估标签为$\hat{y}_i$，那么样本$X_i$的真实标签和预估标签的jaccard相似度
$$
\begin{equation}
\begin{aligned}
J(Y_i,\hat{y}_i) &= \frac{|y_i\cap \hat{y}_i|}{|y_i\cup \hat{y}_i|}\\
& =\frac{|y_i\cap \hat{y}_i|}{|y_i|+|\hat{y}_i|-|y_i\cap \hat{y}_i|}
\end{aligned}
\end{equation}
$$
交集表示两个标签重叠数量，并集是标签的个数。

例子:
A = {0,1,2,5,6}
B = {0,2,3,4,5,7,9}

Solution: J(A,B) = |A∩B| / |A∪B| = |{0,2,5}| / |{0,1,2,3,4,5,6,7,9}| = 3/9 = 0.33.

特点:

jaccard score越大，样本相似度越高

import numpy as np
from sklearn.metrics import jaccard_score
y_true = np.array([[0, 1, 1],
                   [1, 1, 0]])
y_pred = np.array([[1, 1, 1],
                   [1, 0, 0]])

print(jaccard_score(y_true, y_pred, average=None))

print(jaccard_score(y_true, y_pred, average="macro")) # 每一个类别的score平均

print(jaccard_score(y_true, y_pred, average="micro")) # TP/(TP+FP+FN)

Clustering

mutual information score(互信息指数）

给定$N$元素的集合$S{s_1,s_2,…,s_N}$，使用两种方法对$S$进行聚类，得到两个聚类结果：$U={U_1,U_2,…,U_R}$，有$R$个簇；$V={V_1,V_2,…,V_C}$，有$C$个簇。这两个聚类结果满足$\cup_{i=1}^Ru_i=S=\cup_{j=1}^Cv_j$，且对于$U_i,V_j$，任意$i\neq j$，满足
$$
\begin{equation}
\begin{aligned}
U_i\cap U_j=\varnothing = V_i\cap U_j,\
\cup_{i=1}^RU_i = \cup_{j=1}^CV_j = S
\end{aligned}
\end{equation}
$$

设定

$n_{ij}$是簇$U_i$和簇$V_j$共有的元素个数，即$n_{ij}=|U_i\cap V_j|$
$P_U(i)=\frac{|U_i|}{N}$，表示在分类$U$中，任选一个样本，落在簇$U_i$的概率；
$P_V(j)=\frac{|V_j|}{N}$，表示在分类$V$中，任选一个样本，落在簇$V_j$的概率；
$P_{UV}(i,j)=\frac{|U_i\cap V_j|}{N}$为任选一个样本，同时落在簇$U_i$和簇$V_j$的概率

则，互信息指数(MI)的计算如下：
$$
\begin{equation}
\begin{aligned}
\text{MI(U,V)} = \sum\limits_{i=1}^R\sum\limits_{j=1}^CP_{UV}(i,j)\log\frac{P_{UV}(i,j)}{P_U(i)P_V(j)}
\end{aligned}
\end{equation}
$$

normalized_mutual_info_score(标准化互信息)

计算簇$U$的熵（entropy）：
$$
\begin{equation}
\begin{aligned}
H(U)=-\sum\limits_{i=1}^RP_U(i)\log P_U(i)
\end{aligned}
\end{equation}
$$
计算簇$V$的熵（entropy）：
$$
\begin{equation}
\begin{aligned}
H(V)=-\sum\limits_{j=1}^CP_U(j)\log P_U(j)
\end{aligned}
\end{equation}
$$
则标准化互信息(NMI)的计算如下：
$$
\begin{equation}
\begin{aligned}
\text{NMI(U,V)} = \frac{\text{MI(U,V)}}{\sqrt{\text{H(U)H(V)}}}
\end{aligned}
\end{equation}
$$

adjusted mutual info score(调整互信息指数)

wiki

$E{MI(U,V)}$是MI的期望，计算如下
$$
E{MI(U,V)}=\sum\limits_{i=1}^R\sum\limits_{j=1}^C\sum\limits_{n_{ij}=(a_i+b_j-N)^+}^{\min(a_i,b_j)}\frac{n_{ij}}{N}\log(\frac{N\cdot n_{ij}}{a_ib_j})\times \frac{a_i!b_j!(N-a_i)!(N-b_j)!}{N!n_{ij}!(a_i-n_{ij})!(b_j-n_{ij})!(N-a_i-b_j+n_{ij})!}
$$

其中

$(a_i+b_j-N)^+$ 等于 $\max(1, a_i+b_-N)$
$a_i=\sum\limits_{j=1}^C n_{ij}$
$b_j=\sum\limits_{i=1}^R n_{ij}$

那么调整互信息指数计算如下:
$$
AMI(U,V) = \frac{MI(U,V) - E{MI(U,V)}}{\max{H(U),H(V)} - E{MI(U,V)}}
$$

特点

MI是由熵$H(U)$和$H(V)$决定的，量化了两个聚类共享的信息，可以作为聚类相似性的度量
AMI取值范围在[0,1]之间，随机聚类的期望是0，两个聚类完全一样值为1；可用于聚类的评估
AMI需要先验知识（通常这是缺点，但是有了先验知识，评估效果会比较好）
$U$和$V$互换，不影响AMI结果

from sklearn.metrics import mutual_info_score,normalized_mutual_info_score,adjusted_mutual_info_score
y = np.random.randint(0,2, size=(10000))
pred = np.random.randint(0,2, size=(10000))

print(mutual_info_score(y,y)) # 两个一样的划分，互信息指数不等于1
print(mutual_info_score(y,pred)) # 两个随机划分，互信息指数约等于0

print(normalized_mutual_info_score(y,y))
print(normalized_mutual_info_score(y,pred))

print(adjusted_mutual_info_score(y,y)) # 两个一样的划分，AMI=1
print(adjusted_mutual_info_score(y,pred)) # 两个随机划分，AMI=0

adjusted rand score（调整兰德系数）

rand index-兰德系数

给定$n$个元素的集合$S={s_1,s_2,…,s_n}$，使用两种方法对$S$进行聚类，得到两个聚类结果：$U={u_1,u_2,…,u_R}$，有$R$个簇；$V={v_1,v_2,…,v_C}$，有$C$个簇。这两个聚类结果满足$\cup_{i=1}^Ru_i=S=\cup_{j=1}^Cv_j$；对于$u_i,v_j$，任意$i\neq j$，满足
$$
\begin{equation}
\begin{aligned}
u_i\cap u_{j}=\varnothing=v_i\cap v_{j}\\
\cup_{i=1}^Ru_i = \cup_{j=1}^Cv_j = S
\end{aligned}
\end{equation}
$$

假设U是true label, V是聚类结果，设定四个统计量：

$a$是在$U$中为同一类且在$V$中也是同一类的数据点对数
$b$是在$U$中为同一类且在$V$中不是同一类的数据点对数
$c$是在$U$中不为同一类且在$V$中是同一类的数据点对数
$d$是在$U$中不为同一类且在$V$中不是同一类的数据点对数

那么rand index的计算：
$$
\begin{equation}
\begin{aligned}
RI=\frac{a+d}{a+b+c+d}
\end{aligned}
\end{equation}
$$
分母的$a+b+c+d$即在所有样本中任取两个样本:$C_n^2$

问题:两个随机划分的期望并非常数（比如0）

adjusted rand score-调整兰德系数

假设$n_{ij}$表示同在类别$u_i$和簇$v_j$的数据点数目，$n_{i.}$为类$u_i$的数据点数据，$n_{.j}$为簇$v_j$的数目，如下表

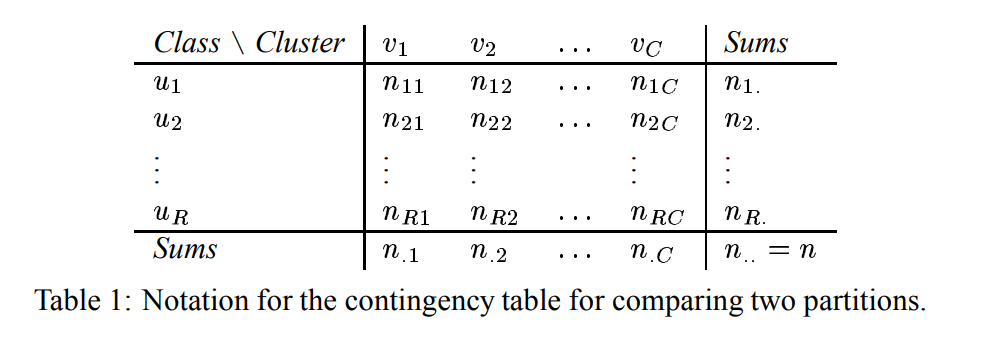
调整的兰德系数为:
$$
\begin{equation}
\begin{aligned}
ARI & = \frac{RI-E(RI)}{\max(RI)-E(RI)}
\end{aligned}
\end{equation}
$$
其中

$RI = \sum_{i,j}(C_{n_{ij}^2})$
$E(RI) = E(\sum_{i,j}(C_{n_{ij}}^2)) = [\sum_i(C_{n_{i.}}^2)\sum_j(C_{n_{.j}}^2)]/(C_n^2)$
$\max(RI)= \frac{1}{2}[\sum_i(C_{n_{i.}}^2) + \sum_j(C_{n_{.j}}^2)]$

特点：

随机划分的期望是0
ARI的范围在[-1,1]，越接近1越好，越接近-1，越差
可用于聚类算法之间的比较
缺点：ARI需要真实类别的标签，在现实中可能不存在这样的数据

from sklearn.metrics import adjusted_rand_score
y = np.random.randint(0,2, size=(10000))
pred = np.random.randint(0,2, size=(10000))

print(adjusted_rand_score(y, pred)) # 两个随机划分，ARI约等于0
print(adjusted_rand_score(pred, y)) # 两者互换，ARI不变

kevin's blog

模型评估方法